Notice
Recent Posts
Recent Comments
Link
250x250
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 기아
- Attention
- 현대자동차
- ODQA
- seaborn
- 2023 현대차·기아 CTO AI 경진대회
- AI Math
- RNN
- pyTorch
- GPT
- matplotlib
- Optimization
- 딥러닝
- mrc
- AI 경진대회
- dataset
- nlp
- N2N
- Transformer
- 데이터 구축
- Self-attention
- Ai
- passage retrieval
- word2vec
- Data Viz
- KLUE
- N21
- Bert
- 데이터 시각화
- Bart
Archives
- Today
- Total
쉬엄쉬엄블로그
(딥러닝) Generative Models - 2 본문
728x90
이 색깔은 주석이라 무시하셔도 됩니다.
Maximum Likelihood Learning

- Given a training set of examples, we can cast the generative model
learning process as finding the best-approximating density model from the model family.- 학습 데이터 샘플들이 주어졌을 때, 생성 모델 학습 과정을 모델 계열에서 가장 근사적인 밀도 모델을 찾는 것으로 볼 수 있음
- Then, how can we evaluate the goodness of the approximation?
- 어떤 기준으로 근사가 잘 되었는지 정의하는 것이 중요
KL-divergence

- 근사적으로 두 분포사이의 거리를 구하는 수식
- We can simplify this with

- As the first term does not depend on $P_\theta$, minimizing the KL-divergence is equivalent to maximizing the expected log-likelihood.
- 첫 번째 항은 $P_\theta$에 의존하지 않기 때문에 $logP_\theta(x)$를 최대화하는 것이 KL-divergence 최소화하는 것과 동일한 효과가 됨

- 첫 번째 항은 $P_\theta$에 의존하지 않기 때문에 $logP_\theta(x)$를 최대화하는 것이 KL-divergence 최소화하는 것과 동일한 효과가 됨
- Approximate the expected log-likelihood with the empirical log-likelihood


- Maximum likelihood learning is then:
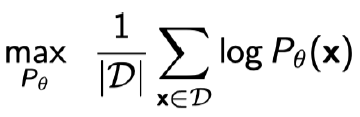
- Variance of Monte Carlo estimate is high

Empirical Risk Minimization
- For maximum likelihood learning, empirical risk minimization (ERM) if often used.
- 최대 우도 학습을 위해 경험적 위험 최소화를 종종 사용함
- However, ERM often suffers from its overfitting.
- 그러나 ERM은 종종 과적합을 겪음
- Extreme case: The model remembers all training data
- 극단적인 경우에 모델은 모든 학습 데이터를 기억함
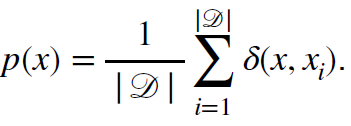
- To achieve better generalization, we typically restrict the hypothesis space of distributions that we search over.
- 더 나은 일반화를 위해 일반적으로 검색하는 분포의 가설 공간을 제한함
- However, it could deteriorate the performance of the generative model.
- 하지만 생성 모델의 성능이 저하될 수 있음
- Usually, MLL is prone to under-fitting as we often use simple parametric distributions such as spherical Gaussians.
- 일반적으로, MLL(Maximum Likelihood Learning)은 구 모양의 가우시안 분포와 같은 단순한 모수 분포를 자주 사용하기 때문에 적합하지 않은 경향이 있음
- What about other ways of measuring the similarity?
- 유사성을 측정하는 다른 방법은?
- KL-divergence leads to maximum likelihood learning or Variational Autoencoder (VAE).
- Jensen-Shannon divergence leads to Generative Adversarial Network (GAN).
- Wasserstein distance leads to Wasserstein Autoencoder (WAE) or Adversarial Autoencoder (AAE).
Latent Variable Models
- D. Kingma, “Variational Inference and Deep Learning: A New Synthesis,” Ph.D. Thesis
Quick Question
- Is an autoencoder a generative model?
- 아님, 오토인코더 자체는 그냥 모델임
Variational Autoencoder
- The objective is simple.
- $\mathbf {Maximize}\ p_\theta(\mathbf x)$
- Variational inference (VI)
- The goal of VI is to optimize the variational distribution that best matches the posterior distribution.
- VI의 목표는 상대적으로 간단하지만 최적화할 수 있는 분포(variational distribution)를 posterior 분포와 비슷하게 만드는 것
- Posterior distribution : $p_\theta(z|x)$
- 데이터가 주어졌을 때 파라미터의 확률 분포
- 계산할 수조차 없음
- Variational distribution : $q_\phi(z|x)$
- 계산은 할 수 있지만 상대적으로 표현력이 떨어짐
- In particular, we want to find the variational distribution that minimizes the KL divergence between the true posterior.
- 특히, 실제 posterior 사이의 KL divergence를 최소화하는 variational 분포를 찾고 싶음
- The goal of VI is to optimize the variational distribution that best matches the posterior distribution.


- Variational Gap은 계산할 수 없기 때문에 무시함
- KL-divergence가 항상 양수이기 때문에 무시할 수 있음
- 그래서 ELBO(Evidence Lower Bound) 파트만 최적화(최대화) 하게 됨
Evidence Lower Bound

- Key Limitation
- It is an intractable model (hard to evaluate likelihood).
- 다루기 어려운 모델임 (우도를 계산하기 힘듬)
- The prior fitting term should be differentiable, hence it is hard to use diverse latent prior distributions.
- prior fitting term은 미분 가능해야 하므로 다양한 잠재 사전 분포(diverse latent prior distribution)를 사용하기 어려움
- KL-divergence가 적분으로 이루어져있고 미분하려면 적분이 풀려야 하기 때문에 계산이 어려움
- In most cases, we use an isotropic Gaussian where we have a closed-form for the prior fitting term.
- 대부분의 경우, prior fitting term에 대해 닫힌 형태를 갖는 등방성 가우시안(isotropic Gaussian)을 사용
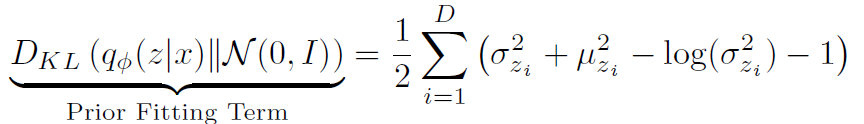
- 대부분의 경우, prior fitting term에 대해 닫힌 형태를 갖는 등방성 가우시안(isotropic Gaussian)을 사용
- It is an intractable model (hard to evaluate likelihood).
Variational Autoencoder

- GAN이 더 좋기 때문에 추천하지는 않는다고 함
Generative Adversarial Networks
- Goodfellow et al., "Generative Adversarial Networks", NIPS, 2014
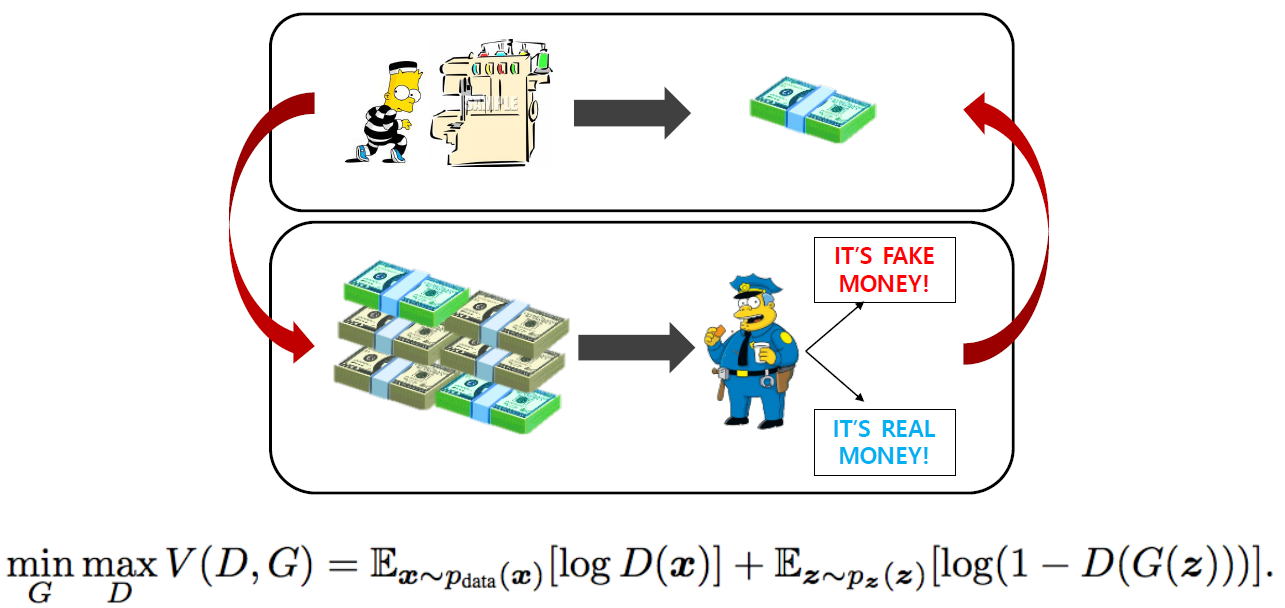
GAN Objective
- GAN is a two player minimax game between generator and discriminator.
- GAN은 생성자와 판별자 간의 minimax game이다.
- Discriminator objective
- 판별자의 목표는 생성자가 만들어낸 이미지인지 실제 이미지인지 판별하는 정확도를 최대화하는 것

- 판별자의 목표는 생성자가 만들어낸 이미지인지 실제 이미지인지 판별하는 정확도를 최대화하는 것
- The optimal discriminator is
- 최적의 판별자 수식

- 최적의 판별자 수식
- Generator objective
- 생성자의 목표는 판별자가 실제 이미지인지 아닌지 판별하는 정확도를 최소화하는 것
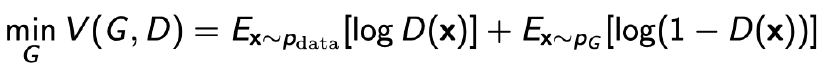
- 생성자의 목표는 판별자가 실제 이미지인지 아닌지 판별하는 정확도를 최소화하는 것
- Plugging in the optimal discriminator, we get
- 최적의 판별자 수식을 적용하면 아래와 같이 Jenson-Shannon Divergence(JSD)의 식이 됨

- 최적의 판별자 수식을 적용하면 아래와 같이 Jenson-Shannon Divergence(JSD)의 식이 됨
Deep Convolutional GAN

Diffusion Models
- Ho et al., "Denoising Diffusion Probabilistic Models," 2020
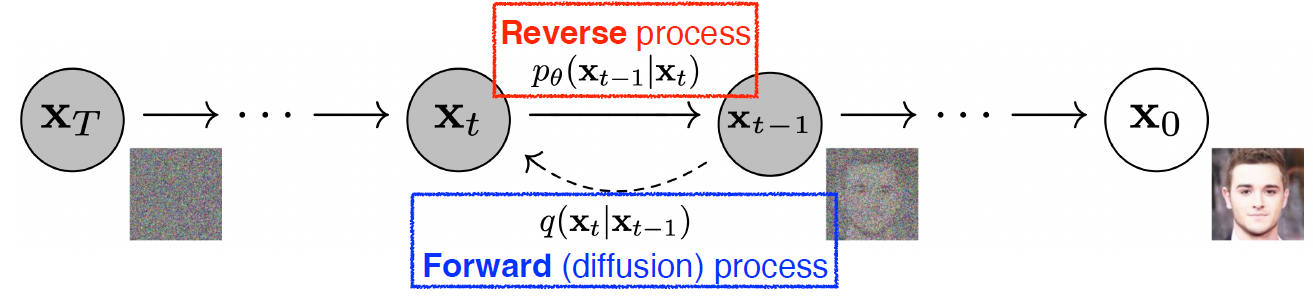
- Diffusion models progressively generate images from noise.
- Diffusion model은 노이즈로부터 이미지를 점진적으로 생성함

- 자세한 설명은 생략
- Forward (diffusion) process progressively injects noise to an image.
- Forward (diffusion) process는 이미지에 노이즈를 점진적으로 주입시킨다.

- Forward (diffusion) process는 이미지에 노이즈를 점진적으로 주입시킨다.
- The reverse process is learned in such a way to denoise the perturbed image back to a clean image.
- reverse process는 교란된 이미지를 깨끗한 이미지로 다시 노이즈를 제거하는 방식으로 학습
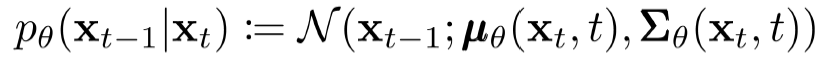
- reverse process는 교란된 이미지를 깨끗한 이미지로 다시 노이즈를 제거하는 방식으로 학습
- 참고 링크
- Diffusion Model은 이미지의 주변 scene에 dependent하고 유사하게 들어갈 수 있는 이미지 편집이 가능함
- GAN 같은 모델은 이미지의 중간만을 편집하는 것이 불가능한 것은 아니지만 Diffusion Model처럼 쉽게 되지는 않음
출처: 부스트캠프 AI Tech 4기(NAVER Connect Foundation)
'부스트캠프 AI Tech 4기' 카테고리의 다른 글
| (Data Viz) Python과 Matplotlib (0) | 2023.06.07 |
|---|---|
| (Data Viz) 시각화의 요소 상태 (2) | 2023.06.06 |
| (딥러닝) Generative Models - 1 (0) | 2023.06.03 |
| (딥러닝) Transformer (0) | 2023.06.02 |
| (딥러닝) Recurrent Neural Networks (0) | 2023.06.01 |
Comments




