Notice
Recent Posts
Recent Comments
Link
250x250
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- AI 경진대회
- GPT
- RNN
- 현대자동차
- AI Math
- KLUE
- Self-attention
- Attention
- Optimization
- pyTorch
- nlp
- Transformer
- N2N
- 딥러닝
- Data Viz
- 기아
- Ai
- matplotlib
- ODQA
- mrc
- passage retrieval
- word2vec
- dataset
- 데이터 구축
- N21
- seaborn
- 2023 현대차·기아 CTO AI 경진대회
- Bert
- 데이터 시각화
- Bart
Archives
- Today
- Total
쉬엄쉬엄블로그
딥러닝에서의 베이즈 통계학 본문
728x90
이 색깔은 주석이라 무시하셔도 됩니다.
조건부 확률이란?
- $P(A\cap B) = P(B)P(A|B)$
- 조건부확률 $P(A|B)$는 사건 $B$가 일어난 상황에서 사건 $A$가 발생할 확률을 의미한다
- 베이즈 정리는 조건부확률을 이용하여 정보를 갱신하는 방법을 알려준다.
- $P(A\cap B)=P(B)P(A|B)$

- $A$라는 새로운 정보가 주어졌을 때 $P(B)$로부터 $P(B|A)$를 계산하는 방법을 제공한다.
- A가 주어졌을 때 B가 일어날 확률을 계산할 때는 A와 B가 동시에 일어날 확률을 A가 일어날 확률로 나눠줌
- 빨간색으로 표시한 부분만 집중해서 보기
베이즈 정리 : 예제

- $\mathcal D$ : 새로 관찰하는 데이터
- $\theta$ : 모델에서 계산하고 싶은 파라미터, 모수, 가설
- 사후확률(posterior) : 데이터를 측정했을 때 이 파라미터가 성립할 확률
- 사전확률(prior) : 데이터가 주어지지 않은 상황에서 모수에 대한 모델링을 하기 이전에 주어진 확률 (데이터를 분석하기 전에 모수에 대해 사전에 가정한 확률 분포)
- 가능도(likelihood) : 현재 주어진 파라미터에서 이 데이터가 관찰될 확률
- Evidence : 데이터 전체의 분포
- COVID-99의 발병률이 10% 로 알려져 있다. COVID-99 에 실제로 걸렸을 때 검진될 확률은 99%, 실제로 걸리지 않았을 때 오검진될 확률이 1% 라고 할 때, 어떤 사람이 질병에 걸렸다고 검진결과가 나왔을 때 정말로 COVID-99에 감염되었을 확률은?
- 사전확률(Prior), 민감도(Recall), 오탐율(False alarm)을 가지고 정밀도(Precision)를 계산하는 문제이다.
- $\theta$를 COVID-99 발병 사건으로 정의(관찰 불가)하고, $\mathcal D$를 테스트 결과라고 정의(관찰 가능)한다.

- 사전확률 : 발병률 10%
- 가능도 : 실제로 걸렸을 때 검진될 확률 99%, 실제로 걸리지 않았을 때 오검진될 확률 1%

- $P(\mathcal D|\neg \theta)$를 모른다면 이 문제를 풀기 어렵다.
- $P(\mathcal D)$ : Evidence
- $\theta$가 일어날 확률 0.1과 $\theta$의 여집합이 일어날 확률 0.9(1 - 0.1)을 가능도(likelihood)에 각각 곱해서 더해주면 Evidence 확률을 계산할 수 있음
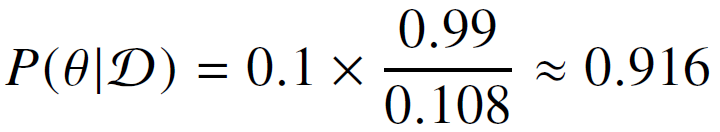
- 만일 오검진될 확률(1종 오류)이 1%가 아닌 10%면 어떻게 될까?
- 오검진될 확률이 10%가 되면 오검진되지 않을 확률이 90%가 된다.
- 오탐율(False alarm)이 오르면 테스트의 정밀도(precision)가 떨어진다.

조건부 확률의 시각화



베이즈 정리를 통한 정보의 갱신
- 베이즈 정리를 통해 새로운 데이터가 들어왔을 때 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산할 수 있다.
출처: boostcourse 인공지능(AI) 기초 다지기(https://www.boostcourse.org/ai100/joinLectures/218531)
'부스트캠프 AI Tech 4기' 카테고리의 다른 글
| RNN 기초 (0) | 2023.05.09 |
|---|---|
| CNN 기초 (0) | 2023.05.08 |
| 딥러닝에서의 통계학 (0) | 2023.05.05 |
| 딥러닝에서의 확률론 (0) | 2023.05.04 |
| 딥러닝 학습방법 (0) | 2023.05.03 |
Comments




