Transformer (cont’d)

Transformer

Transformer : Multi-Head Attention

The input word vectors are the queries, keys and values
- 입력되는 단어 벡터들은 query, key, value로 구성됨
In other words, the word vectors themselves select each other
- 즉, 벡터라는 단어 자체가 서로를 선택함
Problem of single attention
- Only one way for words to interact with one another
  - single attention은 단어들이 서로 상호 작용하는 유일한 방법임
Solution
- Multi-head attention maps $Q,K,V$ into the $h$ number of lower-dimensional spaces via $W$ matrices
  - Multi-head attention은 $W$행렬을 통해 $Q,K,V$를 $h$개의 저차원 공간으로 매핑함
Then apply attention, then concatenate outputs and pipe through linear layer
- 그 다음 attention을 적용하고, 출력과 pipe를 선형 레이어를 통해 연결한다.
  
  $MultiHead(Q, K, V) = Concat(head_1, ..., head_h)W^O$
  $where\ head_i = Attention(QW_i^Q, KW_i^K, VW_i^V)$
Example from illustrated transformer

http://jalammar.github.io/illustrated transformer/
- attention head마다 X벡터와 $W_n^Q,W_n^K,W_n^V$벡터들을 곱해서 $Q_n,K_n,V_n$ 벡터를 구하고 이를 통해 인코딩 벡터 결과 값 $Z_n$을 얻게 됨
- $Z_n$이 Thinking Machines에 해당하는 인코딩 벡터가 됨
- 그러면 각각의 attention head에서 얻어진 결과 벡터들을 concat함
  
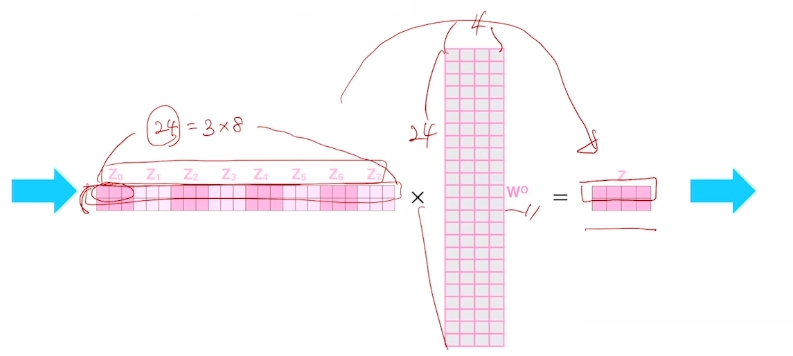
  http://jalammar.github.io/illustrated transformer/
- attention head가 8개이고 각 head별로 3차원 벡터의 출력($Z_n$)들을 concat하면 위 그림처럼 24차원의 결과가 나옴 (attention head 수 * 출력 벡터의 차원 수)
- row vector는 query 단어의 개수인 Thinking Machines에 해당하는 각각의 벡터가 됨
- $W^O$를 통해 차원으로 줄여주는 선형 변환을 수행함
- 그래서 4차원의 벡터($Z$)를 최종적으로 얻게 됨
Maximum path lengths, per-layer complexity and minimum number of sequential operations for different layer types

Attention Is All You Need, NeurIPS’17

Attention Is All You Need, NeurIPS’17
- $n$ is the sequence length
  - $n$은 시퀀스의 길이
- $d$ is the dimension of representation
  - $d$는 표현의 차원 수
- $k$ is the kernel size of convolutions
  - $k$는 컨볼루션의 커널 크기
- $r$ is the size of the neighborhood in restricted self-attention
  - $r$은 restricted self-attention에 있는 이웃의 크기
- Self-Attention 모델은 시퀀스 길이가 아무리 길더라도 GPU 코어수가 충분히 뒷받침된다면 모든 계산을 동시에 수행할 수 있음
- RNN 모델은 $h_{t-1}$을 계산해야만 다음 time step RNN의 입력으로 넣어줄 수 있고 $h_t$를 계산하기 위해서는 $h_{t-1}$이 계산될 때까지 기다릴 수 밖에 없고 Self-Attention처럼 계산이 동시에 수행될 수 없음
- Self-Attention 모델은 학습이 RNN보다 빠르게 진행될 수 있지만 일반적으로 RNN보다 더 많은 메모리를 필요로 하게 됨
- RNN은 가장 끝에 있는 단어가 가장 앞에 있는 단어의 정보를 참조하기 위해서 $n$번의 RNN 레이어를 통과해야 함
  - RNN은 최대 Path Length가 $n$
- 하지만 self-atttention에서는 가장 끝에 있는 단어라도 가장 앞에 있는 단어의 정보를 그냥 인접한 단어와 차이없이 동일하게 key와 value로 보기 때문에 maximum path length가 1임
  - time step이 차이가 많이 나는 단어라도 attention에 기반한 유사도가 높도록 함으로써 정보를 직접적으로 한 번에 가져올 수 있음

Transformer : Block-Based Model

Q, K, V에 $W^Q,W^K,W^V$ 파라미터가 각각 곱해져서 Multi-Head Attention 모듈로 들어가게 됨
즉, 입력 벡터의 값이 연산을 통해 직접 바뀌는 것이 아니기 때문에 모듈 도형이 없음 (Q, K, V에 곱해지는 $W$파라미터들만 갱신되는 것)
Multi-Head Attention 결과로 인코딩 벡터가 나옴
그리고 residual connection(Add) 연산과 layer normarlization(Norm)이 추가적으로 수행됨
그 후 Feed Forward 네트워크를 통과하고 또 residual connection과 layer normalization이 수행됨
Each block has two sub-layers
- 각 블록은 두 개의 하위 레이어를 가짐
- Multi-head attention
- Two-layer feed-forward NN (with ReLU)
Each of these two steps also has
- Residual connection and layer normalization
  - residual connection은 컴퓨터비전쪽에서 깊은 레이어의 뉴럴넷을 만들 때 gradient vanishing 문제를 해결하여 학습을 안정화하고 레이어를 계속 쌓아감에 따라 더 높은 성능을 보일 수 있도록 하는 효과적인 모델
  - residual connection(Add)의 역할
    - 입력 벡터와 Multi-Head Attention의 출력 벡터를 서로 더해주는 연산
    - 결과적으로 Multi-Head Attention 모듈에서는 입력 벡터 대비 만들고자 하는 벡터와의 차이 값을 만들어주는 역할을 함
  - residual connection을 적용하기 위해서 입력 벡터와 encoding된 출력 벡터가 동일한 차원을 가지도록 해야함
    - 그래야 각 차원별로 원소 값을 더해서 동일한 차원을 가지는 벡터를 만들 수 있음
    - 그래서 output layer에 해당하는 선형 변환에서 head 수가 많아짐에 따라 encoding vector의 output들이 concatenate되면서 차원이 늘어나게 되고 그 늘어난 차원을 입력 벡터와 동일한 차원으로 변환하기 위해 $W^o$ 연산을 해줌
- $LayerNorm(x+sublayer(x))$

Transformer : Layer Normalization

Layer normalization changes input to have zero mean and unit variance, per layer and per training point (and adds two more parameters)
- 정규화 레이어는 레이어 및 학습 지점(point) 당 입력이 평균 0, 분산 1을 가지도록 변화시킴(그리고 2개의 파라미터를 추가함)
  
  Group Normalization, ECCV’18
- normalization layer는 주어진 다수의 샘플들에 대해서 그 값들의 평균을 0, 분산을 1로 만들어준 후 우리가 원하는 평균과 분산을 주입할 수 있도록 하는 선형변환(affine transformation)으로 이루어짐
- 가령 batch norm의 경우, 어떤 뉴럴넷이 구성되어 있는 경우에 배치사이즈가 3이라면 입력 레이어에 3차원 벡터를 3개의 데이터 인스턴스에 대해서 넣어줄 것이고 이 때 나온 forward propagation 당시에 특정 노드에서 발생되는(계산되는) 값이 3개 배치 내의 각 데이터 인스턴스에 대해서 3, 5, -2로 나왔다면 특정 레이어의 특정 노드에 발견된 값들에 대해서 이 값들이 어떤 값들이었든지 간에 이 값들의 평균을 0, 분산을 1로 만들어주는 연산을 함
- 즉, normalization 과정은 원래 가지던 값들이 가지는 고유의 평균과 분산이 무슨 값이었든 그 정보를 버리고 표준화된 평균과 분산인 0, 1로 만들어주는 과정이라고 볼 수 있음
- 선형변환 함수가 $y=2x+3$이라면 $x$(입력 벡터들)의 평균이 0, 분산이 1이었을 때, 평균은 3이 되고 분산은 2의 제곱인 4가 됨
  - 위 예제 식에서 나오는 2와 3은 뉴럴넷이 gradient descent에 의해서 최적화하는 파라미터가 됨
  - 뉴럴넷은 학습 과정에서 특정 노드에서 발견되어야 하는 값의 가장 최적화된 평균과 분산을 원하는 만큼 가지도록 조절할 수 있는 방식으로 동작함
Layer normalization consists of two steps
- Normalization of each word vectors to have mean of zero and variance of one.
  - normalization을 통해 각 word vector들의 평균이 0, 분산이 1이 되도록 만듬
- Affine transformation of each sequence vector with learnable parameters.
  - 각 시퀀스 벡터를 학습 파라미터와 함께 선형변환시킴
- layer normalization은 batch norm과 세부적인 차이점은 존재하지만 큰 틀에서는 학습을 안정화하고 최종적인 성능을 끌어올리는데 중요한 역할을 함

Transformer : Positional Encoding

self-attention을 수행할 때 key-value pair들은 순서에 상관없이 각 key별로 주어진 query와의 attention 유사도를 구하고 해당 value vector에 가중치를 부여하여 가중합을 함으로써 주어진 query vector에 대한 encoding vector를 얻는데 주어진 가중 평균을 낼 때 value vector들이 교환 법칙이 성립하기 때문에 최종 output vector는 첫 번째 위치와 세 번째 위치의 결과가 동일하게 됨
- 이러한 순서를 무시한다는 특성은 입력 문장을 sequence 정보를 고려하여 encoding 하지 못하고 순서를 고려하지 않는 집합으로 보고 각 집합 원소의 encoding을 얻는 것과 같아짐
- 이 경우에 RNN과 다른 차이점이 생김
  - RNN은 문장의 단어들이 입력되는 순서가 바뀌면 정보가 적층되는 순서가 달라지기 때문에 encoding vector 결과도 달라지게 됨
  - RNN은 자연스럽게 sequence를 인식하고 이를 구별하여 encoding vector를 얻어낼 수 있는 기법이지만 트랜스포머 혹은 self-attention 모델은 순서 정보를 반영할 수 없는 한계를 가짐
위치에 따라 구별이 될 수 있도록 특정한 상수 벡터를 각 순서에 등장하는 word input vector에 더해주는 것을 positional encoding이라 함
- 그런데 더해주는 상수 벡터를 결정하는 방법이 간단하게 설정되지는 않음
- sin, cos 등으로 이루어진 어떤 주기 함수를 사용함
  - 서로 다른 주기를 써서 여러 sin, cos 함수를 만든 후 거기서 발생된 특정 x 값에서의 함수 값을 모아서 위치를 나타내는 벡터로 사용함
  - 특정한 상수를 만들 때 sin, cos 주기로 만듬
Use sinusoidal functions of different frequencies
- 첫 번째 차원에 해당하는 함수는 sin을 선택하고 이 함수는 위치 정보에 따라 주기가 변하는 형태가 됨
Easily learn to attend by relative position, since for any fixed offset $k$, $PE_{(pos+k)}$ can be represented as linear function of $PE_{(pos)}$
- dim 4는 sin 그래프로 특정한 주기를 가짐
- dim 5는 cos 그래프로 특정한 주기를 가짐
- dim 6은 sin 그래프로 dim 4와 다른 특정한 주기를 가짐
- 위 그림이 sin 및 cos 그래프를 통해 128차원 입력 벡터를 기준으로 만들어짐 (position encoding 벡터를 나타냄)
- 위의 그림처럼 해당 position의 row번째 벡터를 더해주어서 순서를 구분하지 못하는 self-attention 모듈의 한계점을 위치별로 서로 다른 벡터가 더해지도록 함으로써 위치가 달라지면 출력 encoding vector도 달라지도록 만들어줌

Transformer : Warm-up Learning Rate Scheduler

learning rate scheduling
learning rate라는 hyperparameter를 학습 중에 적절히 변경하여 사용하는 것을 learning rate scheduler라 함

Transformer : High-Level View

Attention is all you need, NeurIPS’17
- No more RNN or CNN modules
  
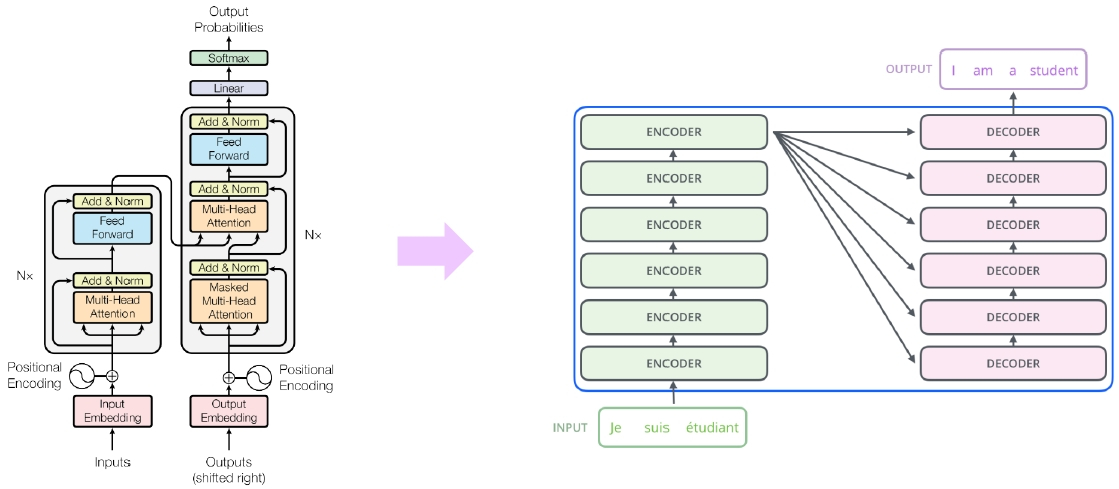
  Attention Is All You Need, NeurIPS’17 / http://jalammar.github.io/illustrated transformer/

Transformer : Encoder Self-Attention Visualization

Words start to pay attention to other words in sensible ways
- 단어들이 다른 단어들에 합리적인 방법으로 attention하기 시작함

https://colab.research.google.com/github/tensorflow/tensor2tensor/blob/master/tensor2tensor/notebooks/hello_t2t.ipynb

Transformer : Decoder

Two sub-layer changes in decoder
- 디코더의 두 sub layer가 변경됨
Masked decoder self-attention on previously generated output
- 이전에 생성된 출력에 대해 masked decoder self-attention 됨
Encoder-Decoder attention, where queries come from previous decoder layer and keys and values come from output of encoder
- Encoder-Decoder attention : query는 이전 디코더 계층에서 들어오고 key와 value는 인코더의 출력에서 들어옴

Transformer : Masked Self-Attention

Those words not yet generated cannot be accessed during the inference time
- 아직 생성되지 않은 단어들에는 inference 시간동안 접근하지 못함
Renormalization of softmax output pervents the model from accessing ungenerated words
- softmax의 renormalization은 모델이 생성되지 않은 단어에 접근하는 것을 막음
- 아래 마지막 그림에서 가중치가 0으로 표현됨

Transformer : Experimental Results

Results on English-German/French translation (newstest2014)

Attention Is All You Need, NeurIPS’17
- BLEU 점수로 봤을 때 낮은 점수라고 생각할 수 있지만 실제 번역된 문장을 보면 체감하는 성능은 좋음

출처: 부스트캠프 AI Tech 4기(NAVER Connect Foundation)