Introduction

생성 모델을 학습한다는 것은 무엇을 의미하는가?

Learning a Generative Model

강아지 이미지들이 주어졌다고 가정해 보자.
모델에 다음과 같은 확률 분포 $p(x)$를 학습시키고자 한다.
- Generation : $\tilde x\sim p(x)$를 샘플링한다면, $\tilde x$는 개처럼 보여야 함
- Density estimation : $x$가 개처럼 보이면 $p(x)$가 높아야 하고 그렇지 않으면 낮아야 함
  - 이를 explicit models라고도 함
그럼, $p(x)$를 어떻게 나타낼까?

Basic Discrete Distributions

Bernoulli distribution(베르누이 분포) : (biased) coin flip (동전 던지기)
- $D$ = {Heads, Tails}
- Specify $P(X=Heads)=p$. Then $P(X=Tails)=1-p$.
- Write : $X\sim Ber(p)$
Categorical distribution : (biased) m-sided dice
- $D$ = {1, …, m}
- Specify $P(Y=i)=p_i$ such that $\sum^m_{i=1}p_i=1$
- Write : $Y\sim Cat(p_1,...,p_m)$
- m개의 면을 갖는 주사위가 존재할 때 m-1개의 파라미터가 필요함
  - 1~m-1까지 확률을 알면 나머지 하나의 확률은 구할 수 있음

Example

RGB 이미지의 단일 픽셀 모델링 (Modeling a single pixel of an RGB image)
- $(r,g,b)\sim p(R,G,B)$
- 경우의 수는?
  - 256 x 256 x 256
- 필요한 파라미터의 수는?
  - 256 x 256 x 256 - 1

Independence

Example

$X_1,...,X_n$ of $n$의 이진 픽셀(흑백 이미지)이 있다고 가정해 보자
- 경우의 수는?
  - $2\times 2 \times \cdots \times 2 = 2^n$
- 필요한 파라미터 수는?
  - $2^n-1$

Structure Through Independence

$X_1,...,X_n$의 이진 픽셀(흑백 이미지)이 독립적이라면 $P(X_1,...,X_n)=P(X_1)P(X_2)\cdots P(X_n)$ 이다.
- 경우의 수는?
  - $2\times 2 \times \cdots \times 2 = 2^n$
- 필요한 파라미터 수는?
  - $n$
    - 파라미터 숫자가 $2^n-1$에서 $n$으로 줄어든 것을 exponential reduction이라고 부름
- $2^n$개의 entries를 $n$개의 수만으로도 표현할 수 있다는 것이 무엇을 의미할까?
  - Independence assumption은 어떤 현상을 모델링할 때 파라미터 수를 굉장히 줄여주는 효과는 있지만 유의미한 분포를 모델링하는 데에는 좋지 않음
  - 그래서 중간 어딘가를 찾고 싶은 것
    - 모든 분포들이 어떤 joint distributed 된 분포가 있고 모든 것이 independent 한 independent assumption이 있으면 그 중간 어딘가에 우리가 원하는 좋은 공간이 있을 것
    - 그런 것들을 표현하기 위해서 Conditional Independence를 활용함

Conditional Independence

Three important rules
- Chain rule
  - $p(x_1,...,x_n)=p(x_1)p(x_2|x1)p(x_3|x_1,x_2)\cdots p(x_n|x1,\cdots ,x_{n-1})$
- Bayes’ rule
  - $p(x|y)=\frac{p(x,y)}{p(y)}=\frac{p(y|x)p(x)}{p(y)}$
- Conditional independence
  - If $x\perp y|z,$ then $p(x|y,z)=p(x|z)$
  - $x\perp y|z$
    - z가 주어졌을 때 x와 y가 independent 하다는 뜻
  - $p(x|y,z)=p(x|z)$
    - y와 z가 모두 주어졌을 때 x에 대한 conditional distribution이 y를 떼어낼 수 있게 된다는 뜻
Chain rule을 활용하면
- $p(X_1,...,X_n)=p(X_1)p(X_2|X1)p(X_3|X_1,X_2)\cdots p(X_n|X1,\cdots ,X_{n-1})$
파라미터 수는?
- $P(X_1)$ : 1 parameter
- $P(X_2|X_1)$ : 2 parameters
  (one per $P(X_2|X_1=0)$ and $P(X_2|X_1=1)$)
- $P(X_3|X_1,X_2)$ : 4 parameters
  - $X_1$과 $X_2$가 각각 앞, 뒤 경우를 가지므로 총 4개의 경우의 수를 가짐
- 따라서 총 파라미터 수는 이전과 동일하게 $1+2+2^2+\cdots+2^{n-1}=2^n-1$ 이다.
- 어째서일까?
$X_{i+1}\perp X_1,...,X_{i-1}|X_i$ (Markov assumption)을 가정하면, $p(x_1,...,x_n)=p(x_1)p(x_2|x_1)p(x_3|x_2)\cdots p(x_n|x_{n-1})$ 이 된다.
파라미터 수는?
- $2n-1$
  - $p(x_1)$을 표현하기 위한 파라미터 수는 1개
  - $p(x_2|x_1$)을 표현하기 위한 파라미터 수는 2개
  - $p(x_3|x_2)$을 표현하기 위한 파라미터 수는 2개
  - 그러므로 1+2+2+…+2(n-1번) = 2n-1
- 따라서 마르코프 가정(Markov assumption)을 활용하여 파라미터의 수를 기하급수적으로 줄일 수 있다.
  - Markov assumption을 가하게 되면 $2^n-1$을 $2n-1$이 됨
  - 그럼 fully indenpendence보다는 크고 independence 조건이 하나도 없는 $2^n$보다는 작게 됨
  - conditional independence 구조를 줌으로써 fully indenpendent와 independent 조건이 하나도 없는 구조 사이 어딘가를 정의할 수 있게 됨
  - 이것이 우리에게 실용적인 구조가 됨
- Autoregressive models는 이러한 조건부 독립성을 활용한다.
  - 이러한 conditional independence 구조를 가장 잘 사용하는 것이 autoregressive models임

Autoregressive Models

28x28 이진 픽셀(흑백 이미지)을 가정해 보자
목표는 $X\in {0,1}^{784}$에서 $P(X)=P(X_1,...,X_{784})$를 배우는 것이다.
그렇다면, $P(X)$를 어떻게 파라미터화 할 수 있을까?
- Chain rule을 사용하여 결합 분포(join distribution)를 인수분해한다.
- 즉,
  - $P(X_{1:784})=P(X_1)P(X_2|X_1)P(X_3|X_2)\cdots$
  - 이를 autoregressive model이라고 부른다.
    - autoregressive model은 항상 임의의 방법으로 2차원 혹은 3차원 공간에 존재하는 이미지를 한 줄로 펴는 ordering 작업이 필요함
  - 모든 무작위 변수의 순서(예: 래스터 스캔 순서)가 필요하다.
    (Note that we need an ordering (e.g., raster scan order) of all random variables.)
    - raster scan order
      - 이미지를 row wise 하게 한 줄로 순서를 메기는 방법

NADE: Neural Autoregressive Density Estimator

$i$번째 픽셀의 확률 분포는 다음과 같다.
- $p(x_i|x_{1:i-1})=\sigma(a_ih_i+b_i)\ where\ h_i=\sigma(W_{{<i}x{1:i-1}}+c)$
NADE는 주어진 입력의 밀도를 계산할 수 있는 명시적(explicit) 모델이다.
- explicit(분명한, 명쾌한) : 단순히 무언가를 생성할 수 있을 뿐만 아니라 어떤 새로운 입력이 주어졌을 때 그 입력(또는 이미지)이 얼마나 모델링하는 것에 유사한지 density를 구할 수 있다는 뜻
BTW, how can we compute the density of the give image?
참고로, 주어진 이미지의 밀도는 어떻게 계산할 수 있을까?
- 784개의 이진 픽셀이 있는 흑백 이미지(즉, ${x_1,x_2,...,x_{784}}$)가 있다고 가정해 보자
- 그러면, 결합 확률(joint probability)은 다음과 같이 계산된다.
  - $p(x_1,...,x_{784})=p(x_1)p(x_2|x_1)\cdots p(x_{784}|x_{1:783})$ where each conditional probability $p(x_i|x_{1:i-1})$ is computed independently
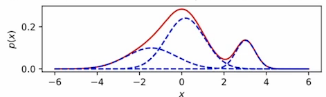
연속 랜덤 변수를 모델링하는 경우 가우스(MoG)의 혼합물을 사용할 수 있다.
(In case of modeling continuous random variables, a mixture of Gaussian (MoG) can be used.)

Summary of Autoregressive Models

Easy to sample from
- Sample $\bar x_0\sim p(x_0)$
- Sample $\bar x_1\sim p(x_1|x_0=\bar x_0)$
- … and so forth (in a sequential manner, hence slow)
- 샘플링이 굉장히 쉬움
- 전체 이미지 혹은 전체 데이터를 한 번에 모델링하기 위해서는 큰 네트워크, 큰 구조가 필요한데 Autoregressive Model은 기본적으로 전체 입력을 dimension별로 쪼개서 모델링하기 때문에 샘플링하기 쉬움
- 미리 정해진 order에 첫 번째 값을 샘플링하고 그 값을 고정한 상태에서 condition distribution을 다음 것으로 샘플링하는 식으로 sequential 하게 샘플링함
- 이미지가 784개 픽셀로 되어있다고 하더라도 샘플링은 784번의 뉴럴 네트워크를 sequential 하게 통과해야 하고 병렬화시킬 수 없음
  - i번째 입력을 만들기 위해서는 i-1번째 입력이 필요하기 때문
  - 그렇기 때문에 생성이 느리다는 단점이 있음
Easy to compute probability $p(x=\bar x)$
- Compute $p(x_0=\bar x_0)$
- Compute $p(x_1=\bar x_1|x_0=\bar x_0)$
- Multiply together (sum their logarithms)
- … and so forth
- Ideally, we can compute all these terms in parallel.
- explicit 한 모델일 때가 많다는 장점이 있음
  - 새로운 이미지가 주어졌을 때 이것에 대한 probability density를 구할 수 없는 경우가 많고 이러한 모델들을 implicit 모델이라고 함
  - 하지만 Autoregressive 모델은 새로운 입력이 주어졌을 때 이것에 대한 joint distribution 혹은 어떤 distribution을 쉽게 구할 수 있게 됨
  - joint distribution을 구하는 것의 장점 중 하나는 각각의 dimension별로 쪼개서 구하는데 쪼개서 구할 때만큼은 병렬화를 할 수 있기 때문에 probability를 계산하는 것이 굉장히 빠름
    - (generation은 오래 걸리지만)
Easy to be extended to continuous variables. For example, we can choose mixture of Gaussians.
- continuous random variables에 확장하기 쉬움
- 기존의 다른 generative 모델들은 discrete와 continouse를 둘 다 고려하는 것이 쉽지 않음
- 하지만 Autoregressive 모델들은 둘 다 고려하는 것을 잘할 수 있다는 장점이 있음

출처: 부스트캠프 AI Tech 4기(NAVER Connect Foundation)